My solution for this problem using “computational method”, by that I mean transforming all geometric properties into computing the ratios of segments, trigonometric functions. There are other solutions using different approachs such that Humpty point’s properties, inversion, or complex numbers.

AoPS link

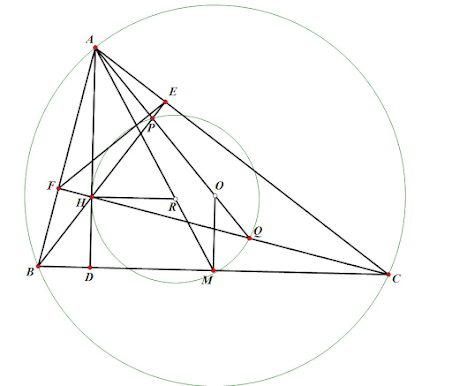
Solution. Let \(M\) be the midpoint of \(BC\) and \(R\) be the center of the circumcircle of triangle \(HPQ\)

Claim 1: \(AH\) is tangent to \(\odot(HPQ)\)

This is just angle chase:

\[\angle AHP=\angle HAB+\angle HBA=90^0-\angle B+90^0-\angle A=\angle C\]

 and

 \(\angle PQH=\angle HCA+\angle CAO=180^0-\angle A-\angle B=\angle C\)

 Claim 2: \(\triangle HPQ \sim \triangle ABC (aa)\)

Cause we have \(\angle PQH=\angle C\), and similarly \(\angle QPH=\angle B\)

Therefore

\[\dfrac{RH}{R_{ABC}}=\dfrac{HP}{AB}=\dfrac{HP}{HA}.\dfrac{HA}{AB}=\dfrac{\sin \angle HAO}{\sin \angle B}.\dfrac{AH}{AB}=\dfrac{\sin \angle B-\angle C}{\sin \angle B}.\dfrac{AH}{AB}\]

 We will prove that \(\dfrac{HR}{HA}=\dfrac{DM}{DA}\) (then apply Thales’ theorem we get the result), which is equivalent to

\(MD=\sin (\angle B-\angle C).R\) \(\Leftrightarrow BC/2-AB.\cos B=\sin (\angle B-\angle C).R\)

\[\Leftrightarrow R.\sin A-2R.\sin C.\cos B=R.(\sin B.\cos C-\cos B.\sin C)\]

 which is true, Q.E.D!