LEARN MATH FOR WHAT? FOR SECURING YOUR COMMUNICATION! (PART 2)

Intro

You can read the Part 1 of the series here Continuing the series of articles on cryptography, today I will introduce you to a very famous type of encryption, which is RSA encryption, created by 3 people Rivest-Shamir-Adleman. RSA was first publicly described in 1977 and has been widely used. However, there is a “devil” that has the potential to attack this encryption algorithm, which is the Quantum Computer. We will explore how the RSA algorithm works, and why quantum computers are now threatening the security of this algorithm.

Asymmetric cryptography

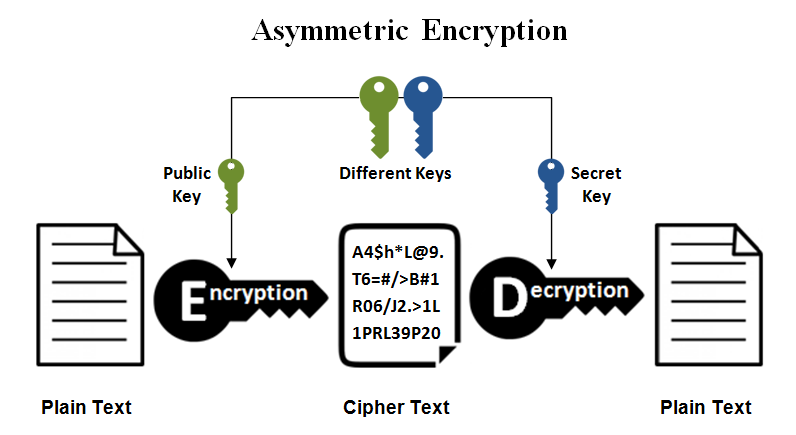RSA is an asymmetric encryption or public-key cryptography: Data will be encrypted with a public key, but can only be decrypted with the private key of the recipient.

We can see that asymmetric encryption algorithms have an advantage in that they have a public key and a private key. Even if an attacker has the public key, they still cannot decrypt the data that has been transmitted.

Other asymmetric encryption algorithms include:

• ECC (Elliptic Curve Cryptography): ECC is an asymmetric encryption algorithm based on the mathematics of elliptic curves. It provides strong security with relatively short key lengths, making it efficient for use in constrained environments such as mobile devices.
• ECDH (Elliptic Curve Diffie-Hellman): similar to ECC, based on the mathematics of elliptic curves
• ElGamal: based on prime numbers and primitive roots

These algorithms will soon be introduced to readers in the following articles.

Motivation behind RSA

We come to the idea behind RSA: RSA is based on the idea that it is extremely difficult to factor a number into its prime factorization. (With the simplest algorithm, the complexity is sqrt(N), with better algorithms such as GNFS (General Number Field Sieve), the complexity is still very large)

The public key consists of two numbers, one of which is the product of two large prime numbers. The private key is also derived from the same two prime numbers.

Therefore, if someone can factor the large number into its prime factors, the private key will be compromised. Therefore, the strength of the encryption lies entirely in the key size and if we double or triple the key size, the strength of the encryption will increase exponentially.

The RSA implementation uses a lot of modular arithmetic, Euler’s theorem, and Euler’s totient function. Note that each step of the algorithm only involves multiplication so computers can easily perform it.

How RSA works

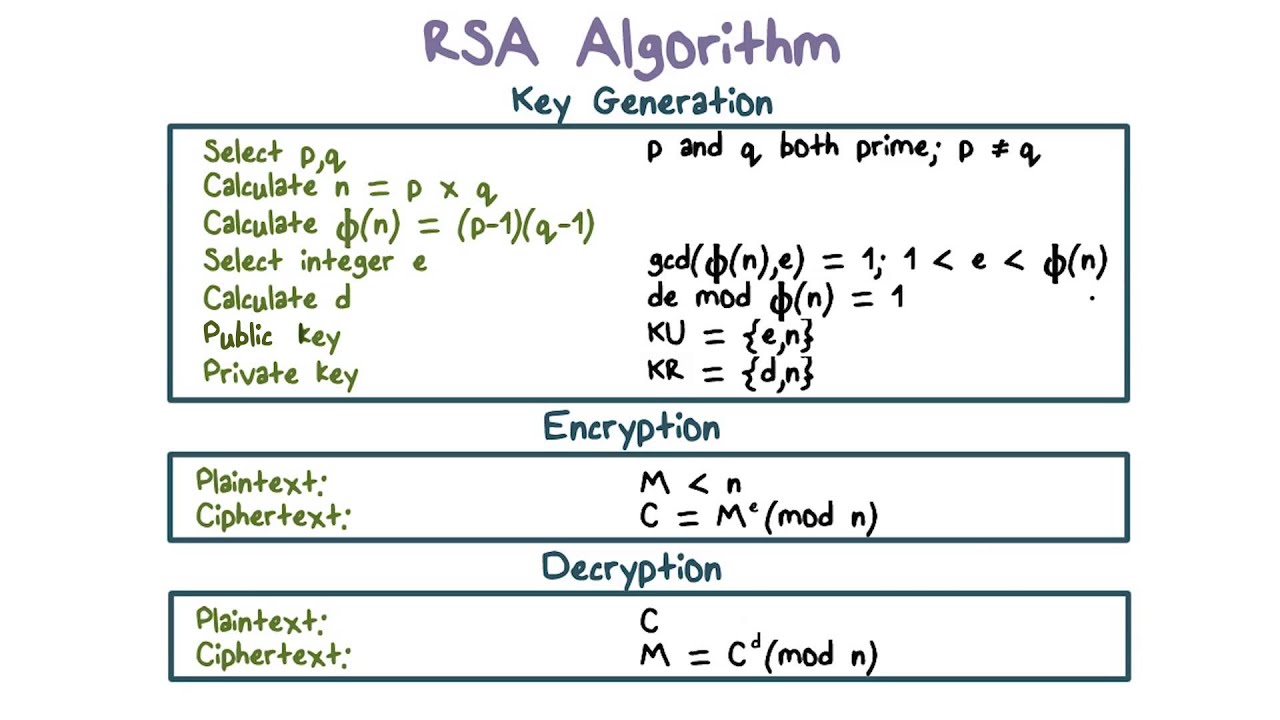(Receiver)

• Choose two large prime numbers, p and q.
• Calculate \(N=p×q\), which will be one half of the first public key.
• Calculate ϕ(N)=(p−1)(q−1) (where ϕ(x) is the number of integers less than x that are relatively prime to x) and choose a number e such that (e,ϕ(N))=1. (In practice, e is often chosen to be 2^16+1=65537, although it can be as small as e=3.) This number e will be the other half of the public key.
• Calculate d, which is the modular inverse of e modulo ϕ(N), meaning that de−1 is divisible by ϕ(N). d will be the private key.
• At this point, the receiver will make the public key (which includes N and e) public, and keep the private key d private.

(Sender)

• Convert the message to a numerical form, typically using the ASCII character set.
• Calculate \(c=m^e (modN)\), which will be the encrypted message (cipher text).
• Send the cipher text c to the receiver. (Receiver)
• Receive the cipher text c.
• Calculate \(m=c^d (modN)\), which will be the original number that the sender sent.
• Translate the number m back to text, to get the original message.

RSA Attacks

To successfully attack RSA, meaning that from \(c=m^e mod N\), N and e, we must recover m, this forces us to know d, where d is the inverse of e mod phi(N); And to calculate phi(N), we must necessarily factor N into p.q

Some ways to attack the RSA algorithm can be listed as follows:

• Trying to factor N into p.q according to the GNFS (General number field sieve) algorithm, the best factorization algorithm on the computers we are using today (Turing machines, the smallest data units are 0,1):

  GNFS is based mainly on Group theory, Ring theory in Abstract Algebra, which is a subject that deals with the closure of multiplication, addition (2 general operations) and its properties in a set.

• Using Shor’s algorithm: This algorithm is based on Euler’s theorem, and the Euclidean algorithm, when used on a conventional computer, the complexity is no faster than GNFS, but when used with a quantum computer, the complexity is much smaller. Why is that?

Shor’s algo works as follows:

• Make a guess r, such that r < N so that they are co-primes of each other.
• Find p such that \(r^p=1 mod N\)
• If p is an odd integer, then go back to Step 1. Else move to the next step.
• Since p is an even integer so, \((r^p/2 – 1)(r^p/2 + 1) = r^p – 1 = 0 mod N=pq\)
• Now, if the value of \(r^p/2 + 1 = 0 mod N\), go back to Step 1.
• If the value of \(r^p/2 + 1 != 0 mod N\), Else move to the next step.
• Compute \(d = gcd(r^p/2+1, N)\).
• The answer required is ‘d’: d is a non-trivial factor of N, from this we can imply the other prime factor by compute N/d

Why Quantum computers are threatening the security of RSA

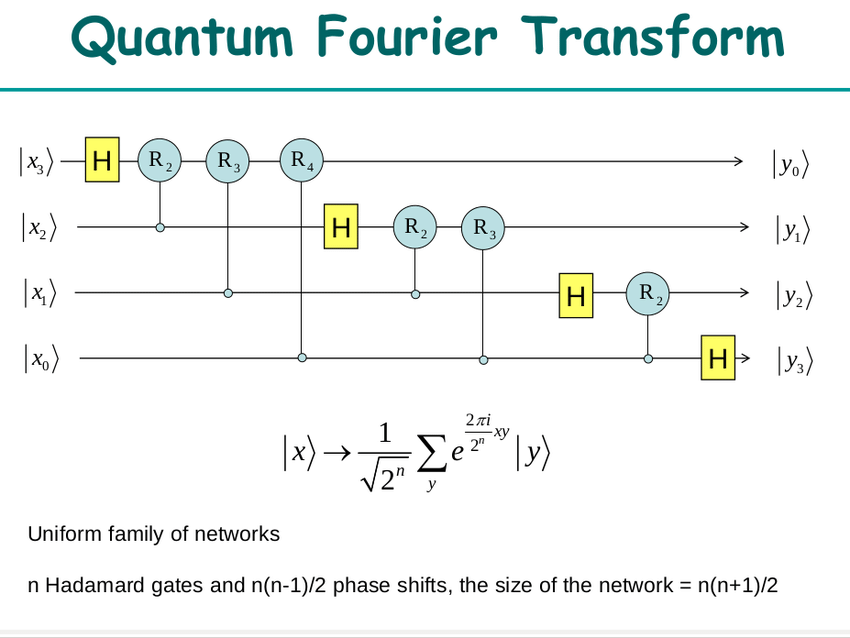So what is special about quantum computers in running Shor’s algorithm?

The answer lies in the fact that quantum bits (Qbits) are not 0 and 1, but can be both 0 and 1 at the SAME TIME, which sounds crazy, right? However, in reality, each Qbit has a superposition, which is mathematically a pair of coefficients representing the probability of the Qbit being 0 or 1.

Although it is in both states at the same time, when we measure it with electromagnetic waves, we will only receive 1 value in the form of a wave.

Based on the periodicity of the function r^x mod N with integer values x, when we measure the values of the Qbits, we will get a table of values. Using the quantum Fourier transform, we will obtain statistics of values with periodicity, from which we can deduce the value of p we need to find!

References

Geeksforgeeks.org

Brilliant.org

Youtube Veritasium

Paper https://www.cs.umd.edu/~gasarch/TOPICS/factoring/NFSmadeeasy.pdf